QUE ES UN CUADRILATERO?

¿Qué es un cuadrilátero?

Un cuadrilátero es una figura geométrica plana que se ubica dentro del tipo de los polígonos.

Está formado por cuatro segmentos de recta que se unen en sus extremos consecutivos dos a dos, en un punto llamado vértice. A su vez, se identifican par de lados opuestos y par de lados consecutivos.

En base a esto, los lados opuestos del cuadrilátero no se unen en ningún vértice y por el contrario, los lados consecutivos, tienen un vértice común.

A su vez, todos los cuadriláteros a su vez, todos los cuadriláteros existentes son cuadrángulos, es decir, polígonos que poseen cuatro ángulos.

Tipos de cuadriláteros

Todos los cuadriláteros se caracterizan por tener cuatro lados, cuatro ángulos y cuatro vértices, sin embargo, su clasificación depende de la medida de los lados y los ángulos.

Existen tres grupos: paralelogramos, trapecios y trapezoides.

Paralelogramos

• Artículo principal: Paralelogramo.

Son cuadriláteros cuyos lados opuestos son paralelos. A este tipo pertenecen:

• Cuadrado: tiene sus cuatros lados de igual longitud y sus cuatro ángulos, cada uno con una amplitud de 90°
• Rectángulo: sus lados paralelos son de igual longitud y sus cuatro ángulos congruentes (90°).
• Rombo: tiene sus cuatro lados congruentes y sus cuatro ángulos son oblicuos.
• Romboide: los ángulos y los lados opuestos son congruentes.



Trapecios

Es un cuadrilátero que tiene solo dos lados paralelos denominados bases. La altura del trapecio es la distancia entre la base mayor y la base menor. Al tipo de trapecios pertenecen:

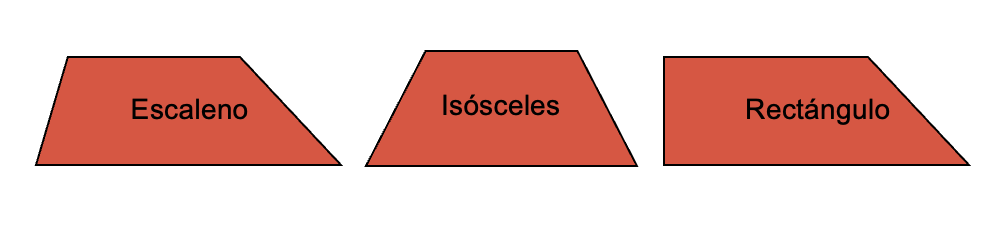
• Escalenos: todos sus lados y ángulos tienen diferente medida.
• Isósceles: sus lados no paralelos son congruentes.
• Rectángulos: dos de sus ángulos interiores son rectos. No debe confundirse con el rectángulo perteneciente al tipo de paralelogramo.



Trapezoides

Son cuadriláteros que no tienen pares de lados paralelos congruentes. Estos pueden ser del tipo:

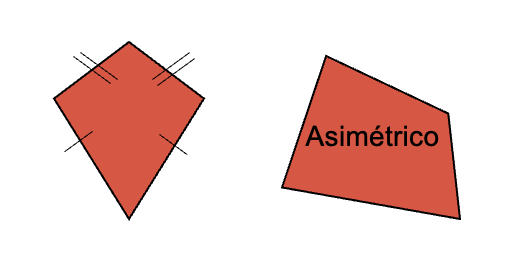
• Simétricos: tienen dos pares de lados consecutivos congruentes.
• Asimétricos: la medida de todos sus lados son diferentes.